
Definition and History
Analytic geometry is defined as the study of geometric problems using coordinate systems to convert them into algebraic problems, it was founded by René Descartes who introduced the Cartesian coordinate system.
The history of analytic geometry dates back to the 17th century when Descartes and Pierre de Fermat developed the method of using coordinates to solve geometric problems.
This method allowed for the solution of complex geometric problems using algebraic techniques, and it laid the foundation for the development of modern mathematics and science.
The definition and history of analytic geometry are well documented in various online resources, including PDF files and academic articles.
These resources provide a detailed account of the development of analytic geometry and its applications in various fields.
The study of analytic geometry has a rich history, and its definition has evolved over time to include various branches of mathematics and science.
Analytic geometry has become a fundamental tool for problem-solving in many fields, including physics, engineering, and computer science.

Key Concepts in Analytic Geometry
Key concepts include coordinate systems, algebraic problems, and vector algebra, available in analytic geometry PDF files for study and reference online.
Coordinate Systems and Algebraic Problems
Coordinate systems are a fundamental concept in analytic geometry, allowing for the representation of geometric problems in algebraic form. This involves using Cartesian coordinates to describe points, lines, and planes in space. Algebraic problems are then used to solve these geometric problems, providing a powerful tool for analysis and solution. The use of coordinate systems and algebraic problems is a key aspect of analytic geometry, and is widely used in many fields, including physics, engineering, and computer science. By representing geometric problems in algebraic form, coordinate systems and algebraic problems provide a flexible and powerful framework for solving a wide range of problems. This approach is widely used in analytic geometry PDF files, providing a useful resource for students and researchers. The combination of coordinate systems and algebraic problems is a key concept in analytic geometry, and is essential for understanding and working with geometric problems.

Applications of Analytic Geometry
Analytic geometry has various applications in physics, engineering, and computer science, solving problems using coordinate systems and algebraic methods, available as PDF files online.
Vector Algebra and Its Applications
Vector algebra is a fundamental concept in analytic geometry, dealing with the study of vectors and their properties. It has numerous applications in describing straight lines, planes, and quadrics in two and three dimensions. The use of skew-angular coordinates and introduction of notations and terminology are essential in vector algebra. This concept is widely used in physics, engineering, and computer science to solve problems and model real-world situations. Analytic geometry pdf files are available online, providing a comprehensive understanding of vector algebra and its applications. These resources include textbooks, lecture notes, and research papers, offering a detailed explanation of the subject matter. By studying vector algebra and its applications, individuals can gain a deeper understanding of analytic geometry and its significance in various fields. The availability of online resources has made it easier for students and researchers to access and learn about this topic.

Study Materials for Analytic Geometry
Study materials for analytic geometry include PDF files, textbooks, and online resources available for free download and study.
PDF Files and Online Resources
PDF files and online resources are widely available for analytic geometry, providing students with a wealth of study materials. These resources include textbooks, lecture notes, and practice problems, all available for free download. Many websites offer PDF files on analytic geometry, covering topics such as coordinate systems, vector algebra, and geometric transformations. Online resources also include interactive tutorials, videos, and quizzes, making it easier for students to understand and apply analytic geometry concepts. Additionally, many online platforms offer PDF files and resources specifically designed for students, including study guides, worksheets, and exam practice materials. With the abundance of PDF files and online resources available, students can easily access and utilize these materials to support their learning and understanding of analytic geometry. These resources are convenient, accessible, and free, making them an ideal supplement to traditional classroom instruction and textbook materials.
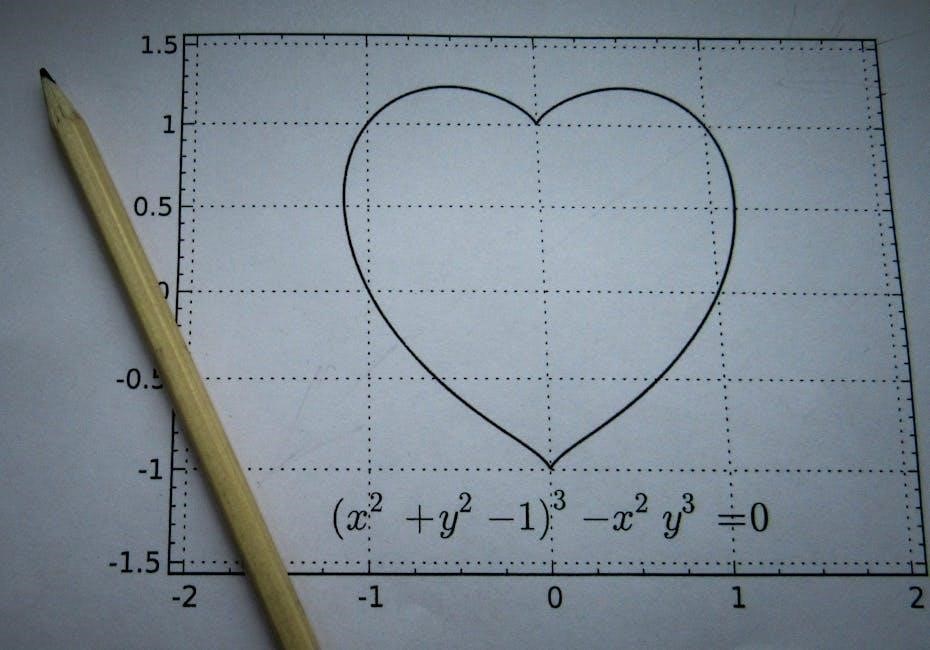
Importance of Analytic Geometry
The importance of analytic geometry lies in its ability to solve complex geometric problems using algebraic methods, making it a crucial tool in various fields such as physics, engineering, and computer science.
The study of analytic geometry provides a strong foundation for understanding and analyzing geometric shapes and structures, which is essential for many real-world applications.
By using coordinate systems and algebraic equations, analytic geometry enables us to model and simulate complex systems, making it a vital component of modern science and technology.
The availability of analytic geometry study materials online, including PDF files and other digital resources, has made it easier for students and researchers to access and learn about this important subject.
Overall, the importance of analytic geometry cannot be overstated, as it has far-reaching implications for many areas of study and has the potential to solve some of the most complex problems in mathematics and science.